Atom (measure theory)
In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure. A measure which has no atoms is called non-atomic or atomless.
Contents |
Definition
Given a measurable space 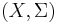 and a measure
and a measure  on that space, a set
on that space, a set  in
in  is called an atom if
is called an atom if
and for any measurable subset  of
of  with
with
one has 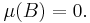
Examples
- Consider the set X={1, 2, ..., 9, 10} and let the sigma-algebra
 be the power set of X. Define the measure
be the power set of X. Define the measure  of a set to be its cardinality, that is, the number of elements in the set. Then, each of the singletons {i}, for i=1,2, ..., 9, 10 is an atom.
of a set to be its cardinality, that is, the number of elements in the set. Then, each of the singletons {i}, for i=1,2, ..., 9, 10 is an atom. - Consider the Lebesgue measure on the real line. This measure has no atoms.
Non-atomic measures
A measure which has no atoms is called non-atomic. In other words, a measure is non-atomic if for any measurable set  with
with 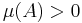 there exists a measurable subset B of A such that
there exists a measurable subset B of A such that
A non-atomic measure with at least one positive value has an infinite number of distinct values, as starting with a set A with 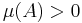 one can construct a decreasing sequence of measurable sets
one can construct a decreasing sequence of measurable sets
such that
This may not be true for measures having atoms; see the first example above.
It turns out that non-atomic measures actually have a continuum of values. It can be proved that if μ is a non-atomic measure and A is a measurable set with 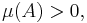 then for any real number b satisfying
then for any real number b satisfying
there exists a measurable subset B of A such that
This theorem is due to Wacław Sierpiński.[1][2] It is reminiscent of the intermediate value theorem for continuous functions.
Sketch of proof of Sierpiński's theorem on non-atomic measures. A slightly stronger statement, which however makes the proof easier, is that if 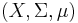 is a non-atomic measure space and
is a non-atomic measure space and 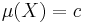 , there exists a function
, there exists a function ![S:[0, c]\to\Sigma](/2012-wikipedia_en_all_nopic_01_2012/I/bbd294b59921de8393835fa7e3861b4d.png) that is monotone with respect to inclusion, and a right-inverse to
that is monotone with respect to inclusion, and a right-inverse to ![\mu:\Sigma\to[0,\,c]](/2012-wikipedia_en_all_nopic_01_2012/I/4636cfb4236d7dca6170b03f3d0bfe35.png) . That is, there exists a one-parameter family of measurable sets S(t) such that for all
. That is, there exists a one-parameter family of measurable sets S(t) such that for all 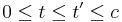
The proof easily follows from Zorn's lemma applied to the set of all monotone partial sections to  :
:
ordered by inclusion of graphs, 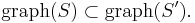 It's then standard to show that every chain in
It's then standard to show that every chain in  has a maximal element, and that any maximal element of
has a maximal element, and that any maximal element of  has domain
has domain ![[0,c],](/2012-wikipedia_en_all_nopic_01_2012/I/f340015571f487c94dae8363a61fda46.png) proving the claim.
proving the claim.
See also
- Atom (order theory) — an analogous concept in order theory
- Dirac delta function
- Elementary event, also known as an atomic event
Notes
- ^ Sierpinski, W. (1922). "Sur les fonctions d'ensemble additives et continues". Fundamenta Mathematicae 3: 240–246. http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3125.pdf.
- ^ Fryszkowski, Andrzej (2005). Fixed Point Theory for Decomposable Sets (Topological Fixed Point Theory and Its Applications). New York: Springer. p. 39. ISBN 1-4020-2498-3.
References
- Bruckner, Andrew M.; Bruckner, Judith B.; Thomson, Brian S. (1997). Real analysis. Upper Saddle River, N.J.: Prentice-Hall. p. 108. ISBN 0-13-458886-X.
- Butnariu, Dan; Klement, E. P. (1993). Triangular norm-based measures and games with fuzzy coalitions. Dordrecht: Kluwer Academic. p. 87. ISBN 0-7923-2369-6.
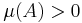
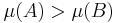
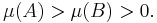
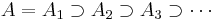
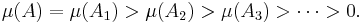
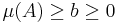
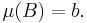
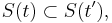
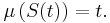
![\Gamma:=\{S:D\to\Sigma\;�:\; D\subset[0,\,c],\, S\; \mathrm{ monotone }, \forall t\in D\; (\mu\left (S(t)\right)=t)\},](/2012-wikipedia_en_all_nopic_01_2012/I/8dc85b057fdcbfd87e377c1cc205a2c9.png)